2 Chapter 2 exercises

    1. Compute \(\pi + \text{e}\), where \(\pi = 3.1415927 \times 10^0\) and \(\text{e} = 2.7182818 \times 10^0\), using floating point addition in base 10, working to five decimal places.

      Solution

      As \(\pi\) and \(\text{e}\) have a common exponent, we sum their mantissas, i.e. \[\begin{align*} \pi + \text{e} &= (3.14159 \times 10^0) + (2.71828 \times 10^0)\\ &= 5.85987 \times 10^0 \end{align*}\]

    2. Now compute \(10^6\pi + \text{e}\), using floating point addition in base 10, now working to seven decimal places.

      Solution

      We first need to put the numbers on a common exponent, which is that of \(10^6 \pi\). \[\begin{align*} 10^6 \pi &= 3.1415927 \times 10^6\\ \text{e} & = 2.7182818 \times 10^0 = 0.0000027 \times 10^6. \end{align*}\] Then summing their mantissas gives \[\begin{align*} 10^6 \pi + \text{e} &= (3.1415927 \times 10^6) + (2.7182818 \times 10^0)\\ &= (3.1415927 \times 10^6) + (0.0000027 \times 10^6)\\ &= (3.1415927 + 0.0000027) \times 10^6\\ &= 3.1415954 \times 10^6. \end{align*}\]

    3. What would happen if we computed \(10^6\pi + \text{e}\) using a base 10 floating point representation, but only worked with five decimal places?

      Solution

      If we put \(2.7182818 \times 10^0\) onto the exponent \(10^6\) we get \(0.00000 \times 10^6\) to five decimal places, and so \(\text{e}\) becomes negligible alongside \(10^6 \pi\) if we only work to five decimal places.

  2. Write \(2\pi\) in binary form using single- and double precision arithmetic. [Hint: I recommend you consider the binary forms for \(\pi\) given in the lecture notes, and you might also use bit2decimal() from the lecture notes to check your answer.]

    Solution

    The key here is to note that we want to calculate \(\pi \times 2\). As we have a number in the form \(S \times (1 + F) \times 2^{E - e}\), then we just need to raise \(E\) by one. For both single- and double-precision, this corresponds to changing the last zero in the 0s and 1s for the \(E\) term to a one.

    bit2decimal <- function(x, e, dp = 20) {
# function to convert bits to decimal form
# x: the bits as a character string, with appropriate spaces
# e: the excess
# dp: the decimal places to report the answer to
bl <- strsplit(x, ' ')[[1]] # split x into S, E and F components by spaces
# and then into a list of three character vectors, each element one bit
bl <- lapply(bl, function(z) as.integer(strsplit(z, '')[[1]]))
names(bl) <- c('S', 'E', 'F') # give names, to simplify next few lines
S <- (-1)^bl$S # calculate sign, S
E <- sum(bl$E * 2^c((length(bl$E) - 1):0)) # ditto for exponent, E
F <- sum(bl$F * 2^(-c(1:length(bl$F)))) # and ditto to fraction, F
z <- S * 2^(E - e) * (1 + F) # calculate z
out <- format(z, nsmall = dp) # use format() for specific dp
# add (S, E, F) as attributes, for reference
attr(out, '(S,E,F)') <- c(S = S, E = E, F = F)
out
}
bit2decimal('0 10000001 10010010000111111011011', 127)
    ## [1] "6.28318548202514648438"
## attr(,"(S,E,F)")
##           S           E           F 
##   1.0000000 129.0000000   0.5707964
    bit2decimal('0 10000000001 1001001000011111101101010100010001000010110100011000', 1023)
    ## [1] "6.28318530717958623200"
## attr(,"(S,E,F)")
##            S            E            F 
##    1.0000000 1025.0000000    0.5707963

  3. Find the calculation error in R of \(b - a\) where \(a = 10^{16}\) and \(b = 10^{16} + \exp(0.5)\).

    Solution 
    a <- 1e16
b <- 1e16 + exp(.5)
b - a
    ## [1] 2

  4. Create the following: The row vector \[ \mathbf{a} = (2, 4, 6), \] the \(2 \times 3\) matrix \[ \mathbf{B} = \left(\begin{array}{ccc} 6 & 5 & 4\\ 3 & 2 & 1\end{array}\right) \] and a list with first element \(\mathbf{a}\) and second element \(\mathbf{B}\), and an arbitrary (i.e. with whatever values you like) \(5 \times 3 \times 2\) array with a 'name' attribute that is 'array1'. \(~\)
    For each of the above, consider whether your code could be simpler.

    Solution 
    a <- t(c(2, 4, 6))
B <- matrix(6:1, 2, byrow = TRUE)
l <- list(a, B)
arr <- array(rnorm(30), c(5, 3, 2))
attr(arr, 'name') <- 'array1'
arr
    ## , , 1
## 
##            [,1]        [,2]       [,3]
## [1,] -0.1665812  0.05562442  0.6567512
## [2,] -0.3405456 -0.55061824 -1.2692691
## [3,]  0.2649471 -0.28015988  1.2724331
## [4,] -0.9606964  0.32101714  0.8776822
## [5,] -0.4040439  0.51386765 -0.6041180
## 
## , , 2
## 
##            [,1]       [,2]       [,3]
## [1,] -1.4899078 -1.6131559 0.07536778
## [2,]  0.1407264  0.5466237 0.22770119
## [3,]  0.5799854 -1.1506912 0.60413031
## [4,] -1.1158511 -1.7293453 0.59833274
## [5,] -0.6673627 -0.5074252 0.59765211
## 
## attr(,"name")
## [1] "array1"

  5. Produce a \(3 \times 4 \times 4 \times 2\) array containing Uniform(0, 1) random variates and compute the mean over its second and third margins using apply(..., ..., means) and rowMeans() or colMeans().

    Solution 
    arr <- array(NA, c(3, 4, 4, 2))
arr[] <- runif(prod(dim(arr))) # saves names to get the number right
apply(arr, 2:3, mean)
    ##           [,1]      [,2]      [,3]      [,4]
## [1,] 0.6598318 0.3636343 0.5869241 0.4264603
## [2,] 0.4855723 0.5240322 0.4078280 0.5484461
## [3,] 0.2890008 0.5000593 0.3627857 0.4479420
## [4,] 0.4775275 0.3867275 0.4655408 0.3439320
    rowMeans(aperm(arr, c(2, 3, 1, 4)), dims = 2)
    ##           [,1]      [,2]      [,3]      [,4]
## [1,] 0.6598318 0.3636343 0.5869241 0.4264603
## [2,] 0.4855723 0.5240322 0.4078280 0.5484461
## [3,] 0.2890008 0.5000593 0.3627857 0.4479420
## [4,] 0.4775275 0.3867275 0.4655408 0.3439320
    colMeans(aperm(arr, c(1, 4, 2, 3)), dims = 2)
    ##           [,1]      [,2]      [,3]      [,4]
## [1,] 0.6598318 0.3636343 0.5869241 0.4264603
## [2,] 0.4855723 0.5240322 0.4078280 0.5484461
## [3,] 0.2890008 0.5000593 0.3627857 0.4479420
## [4,] 0.4775275 0.3867275 0.4655408 0.3439320

    1. Create a 3-element list of vectors comprising Uniform(0, 1) variates of length 3, 5 and 7, respectively.

      Solution 
      lst <- list(runif(3), runif(5), runif(7))

    2. Create another list in which the vectors above are sorted into descending order.

      Solution 
      lst2 <- lapply(lst, sort, decreasing = TRUE)

    3. Then create a vector comprising the minimum of each vector in the list, and another stating which element is the minimum. [Hint: for the latter you may want to consult the ‘See Also’ part of the min() function’s help file.]

      Solution 
      sapply(lst, min)
      ## [1] 0.22358422 0.40101038 0.05418506
      sapply(lst, which.min)
      ## [1] 3 5 5

  7. Use a for() loop to produce the following. [Hint: the function paste() might be useful.]

    ## [1] "iteration 1"
## [1] "iteration 2"
## [1] "iteration 3"
## [1] "iteration 4"
## [1] "iteration 5"
## [1] "iteration 6"
## [1] "iteration 7"
## [1] "iteration 8"
## [1] "iteration 9"
## [1] "iteration 10"
    Solution 
    for (i in 1:10) print(paste('iteration', i))
    ## [1] "iteration 1"
## [1] "iteration 2"
## [1] "iteration 3"
## [1] "iteration 4"
## [1] "iteration 5"
## [1] "iteration 6"
## [1] "iteration 7"
## [1] "iteration 8"
## [1] "iteration 9"
## [1] "iteration 10"

  8. Consider the following two infinite series that represent \(\pi\).\[\begin{align*} \pi &= 4 \left[1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \frac{1}{11} + \frac{1}{13} -\cdots\right]\\ \pi &= 3 + \frac{4}{2 \times 3 \times 4} - \frac{4}{4 \times 5 \times 6} + \frac{4}{6 \times 7 \times 8} - \frac{4}{8 \times 9 \times 10} + \cdots \end{align*}\] Use a while() loop to find which converges to pi in R to within \(\epsilon_m^{1/3}\) using the fewest terms, where \(\epsilon_m\) is R’s machine tolerance.

    Solution

    Here’s the first approximation…

    quarter_pi <- 1
terms1 <- 1
denom <- 3
multiplier <- -1
my_pi <- 4 * quarter_pi
while(abs(my_pi - pi) > .Machine$double.eps^(1/3)) {
  terms1 <- terms1 + 1
  quarter_pi <- quarter_pi + multiplier / denom
  my_pi <- 4 * quarter_pi
  denom <- denom + 2
  multiplier <- -1 * multiplier
}
terms1
    ## [1] 165141

    …and here’s the second approximation…

    my_pi <- 3
terms2 <- 2
denoms <- c(2, 3, 4)
multiplier <- 1
while(abs(my_pi - pi) > .Machine$double.eps^(1/3)) {
  my_pi <- my_pi + multiplier * 4 / prod(denoms)
  denoms <- denoms + 2
  multiplier <- -1 * multiplier
  terms2 <- terms2 + 1
}
terms2
    ## [1] 36

    1. Write a function based on a for() loop to calculate the cumulative sum of a vector, \(\bf y\), i.e. so that its \(i\)th value, \(y_i\) say, is \[y_i = \sum_{j = 1}^i x_j.\]

      Solution

      Either of the following two functions are options (although others exist).

      my_cumsum <- function(x) {
# function 1 to calculate cumulative sum of a vector
# x is a vector
# returns a vector of length length(x)
out <- numeric(length(x))
for (i in 1:length(x)) {
  out[i] <- sum(x[1:i])
}
out
}

my_cumsum2 <- function(x) {
# function 2 to calculate cumulative sum of a vector
# x is a vector
# returns a vector of length length(x)
out <- x
for (i in 2:length(x)) {      
  out[i] <- out[i] + out[i - 1]
}
out
}

      We see that both perform the same calculation.

      x <- runif(10)
cumsum(x)
      ##  [1] 0.8291765 1.6531608 1.7352366 1.8885832 2.3897789 3.0083146 3.4798496 3.5285217 4.3646237 5.1984644
      my_cumsum(x)
      ##  [1] 0.8291765 1.6531608 1.7352366 1.8885832 2.3897789 3.0083146 3.4798496 3.5285217 4.3646237 5.1984644
      my_cumsum2(x)
      ##  [1] 0.8291765 1.6531608 1.7352366 1.8885832 2.3897789 3.0083146 3.4798496 3.5285217 4.3646237 5.1984644

    2. Then benchmark its execution time against R’s vectorised function cumsum() for summing 1000 iid \(Uniform[0, 1]\) random variables.

      Solution 
      x <- runif(1e3)
microbenchmark::microbenchmark(
  cumsum(x),
  my_cumsum(x),
  my_cumsum2(x)
)
      ## Unit: nanoseconds

    1. To start a board game, a player must throw three sixes using a conventional die. Write a function to simulate this, which returns the total number of throws that the player has taken.

      Solution 
      sixes1 <- function() {
# function to simulate number of throws needed
# to reach three sixes
# n is an integer
# returns total number of throws taken
out <- sample(1:6, 3, replace = TRUE)
while(sum(out == 6) < 3) {
  out <- c(out, sample(1:6, 1))
}
return(length(out))
}

    2. Then use 1000 simulations to empirically estimate the distribution of the number of throws needed.

      Solution 
      samp1 <- replicate(1e3, sixes1())
table(samp1)
      ## samp1
##  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 47 49 50 52 56 58 61 
##  2  9 17 32 33 36 37 57 44 47 42 46 53 41 47 37 47 30 43 34 21 29 21 26 20 11 13 19 13 12  6 10  7  8  6  6  6  3  7  5  1  2  3  2  4  1  1  1  1  1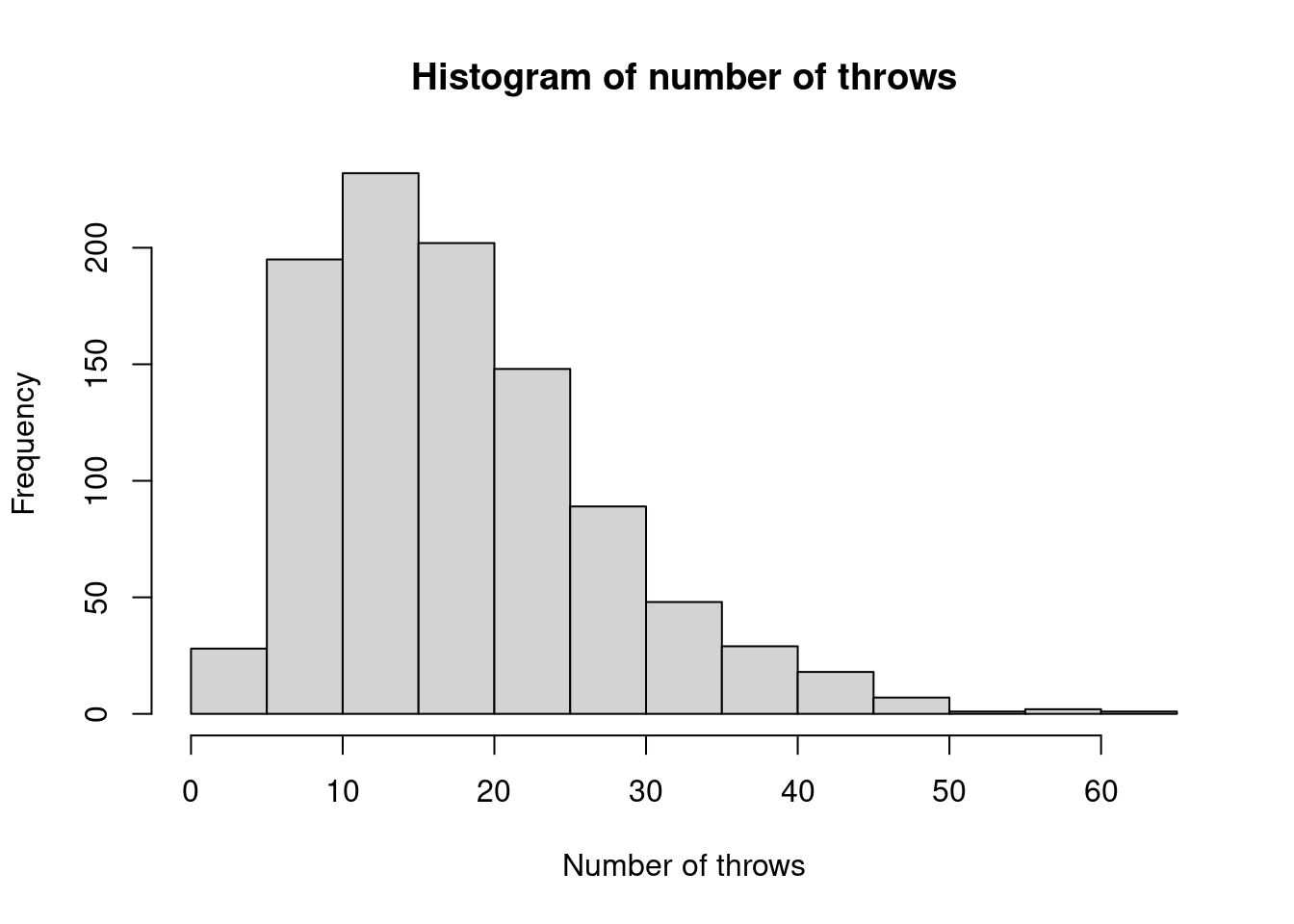
      hist(samp1, xlab = 'Number of throws', main = 'Histogram of number of throws')
      Histogram of empirical distribution of number of throws for starting method 1.

      Figure 2.1: Histogram of empirical distribution of number of throws for starting method 1.

    3. I think you’ll agree that this would be a rather dull board game! It is therefore proposed that a player should instead throw two consecutive sixes. Write a function to simulate this new criterion, and estimate its distribution empirically.

      Solution 
      sixes2 <- function() {
# function to simulate number of throws needed
# for two consecutive sixes
# n is an integer
# returns total number of throws taken
out <- sample(1:6, 2, replace = TRUE)
cond <- TRUE
while(cond) {
  if (sum(out[1:(length(out) - 1)] + out[2:length(out)] == 12) > 0) {
    cond <- FALSE
  } else {
    out <- c(out, sample(1:6, 1))
  }
}
return(length(out))
}
sixes2()
      ## [1] 2

    4. Then use 1000 simulations to empirically estimate the distribution of the number of throws needed.

      Solution 
      samp2 <- replicate(1e3, sixes2())
table(samp2)
      ## samp2
##   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19  20  21  22  23  24  25  26  27  28  29  30  31  32  33  34  35  36  37  38  39  40  41  42  43  44  45 
##  30  17  26  21  18  20  42  17  20  25  20  14  16  12  16  15  12  16   8  20  14  10  14   8  10  17  14  12  11  12  16  10  16   9  14  10   8  12   6   7   6  14  11  11 
##  46  47  48  49  50  51  52  53  54  55  56  57  58  59  60  61  62  63  64  65  66  67  68  69  70  71  72  73  74  75  76  78  79  80  81  82  83  84  85  86  87  88  89  90 
##   9   7   5  11   9   3   8   7   5   9   6   2   7   4   5   4   9   7   5   9   3   8   3   3   4   6   8   6   5   2   8   4   5   1   7   2   5   4   2   2   8   1   4   6 
##  91  92  93  94  96  97  98  99 100 101 103 104 105 106 107 108 109 110 111 112 113 115 117 118 119 120 121 122 124 125 129 131 133 134 135 139 142 143 144 146 152 153 160 165 
##   1   4   1   1   1   5   3   3   1   1   4   2   2   1   2   3   4   5   1   3   1   4   1   1   1   2   1   3   2   1   2   1   1   3   1   3   2   1   2   3   1   1   1   1 
## 168 172 175 179 180 189 191 201 202 204 208 213 235 239 327 372 
##   1   1   1   1   1   1   1   1   1   1   1   1   1   1   2   1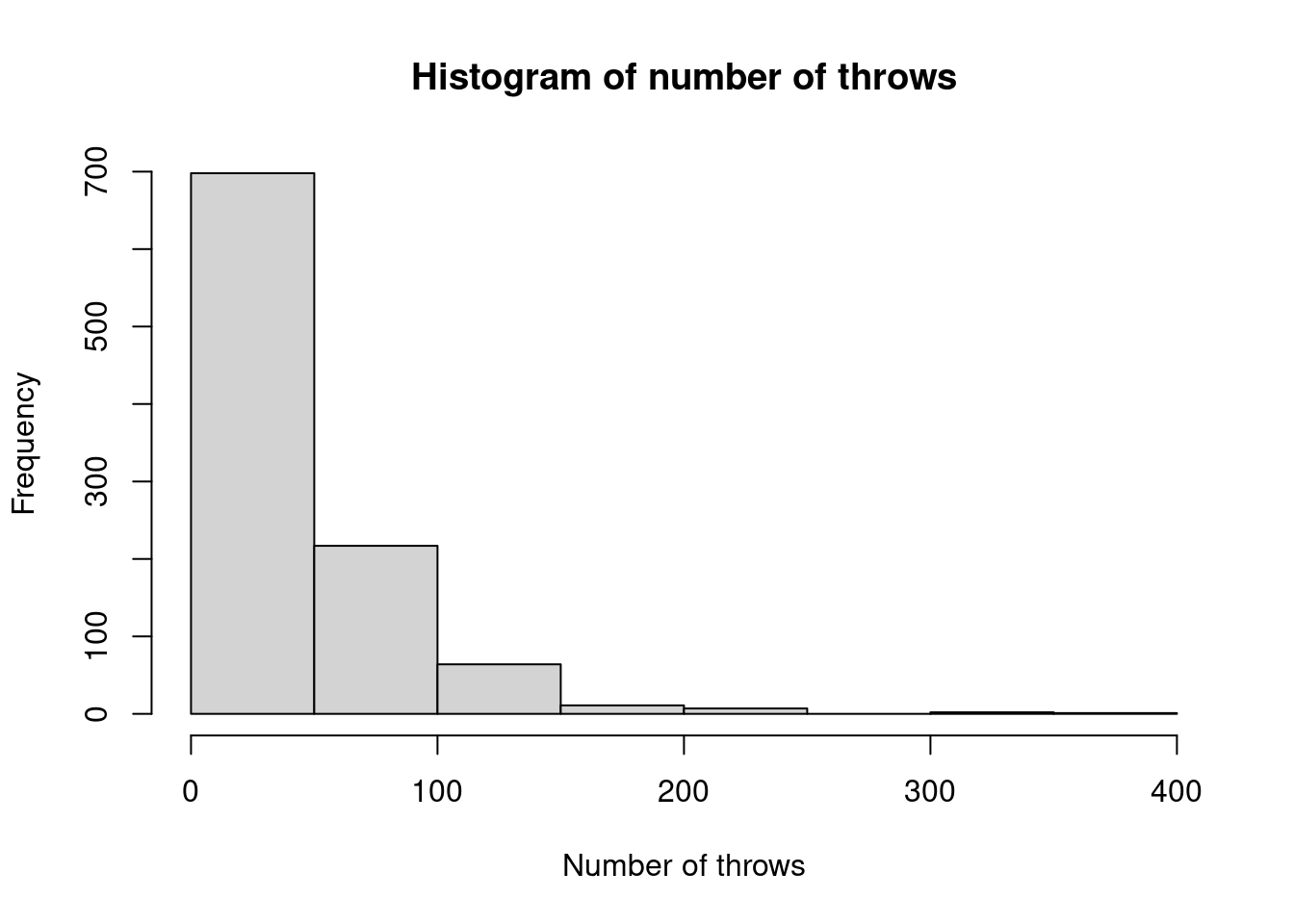
      hist(samp2, xlab = 'Number of throws', main = 'Histogram of number of throws')
      Histogram of empirical distribution of number of throws for starting method 2.

      Figure 2.2: Histogram of empirical distribution of number of throws for starting method 2.

    5. By comparing sample mean starting numbers of throws, which starting criterion should get a player into the game quickest?

      Solution 
      mean(samp1) - mean(samp2)
      ## [1] -24.2

      So the second approach, by comparing means, takes more throws before the game can begin.

  11. Consider the following two functions for calculating \[d_i = x_{i + 1} - x_i, \hspace{2cm} i = 1, \ldots, n - 1\] where \({\bf x}' = (x_1, \ldots, x_n)\).

    diff1 <- function(x) {
# function to calculate differences of a vector
# based on a for loop
# x is a vector
# returns a vector of length (length(x) - 1)
out <- numeric(length(x) - 1)
for (i in 1:(length(x) - 1)) {
  out[i] <- x[i + 1] - x[i]
}
out
}
    diff2 <- function(x) {
# function to calculate differences of a vector
# based on vectorisation
# x is a vector
# returns a vector of length (length(x) - 1)
id <- 1:(length(x) - 1)
x[id + 1] - x[id]
}

    The first, diff1() uses a straightforward for() loop to calculate \(d_i\), for \(i = 1, \ldots, n - 1\), whereas diff2() could be seen to be a vectorised alternative. Benchmark the two for a vector of \(n = 1000\) iid \(N(0, 1)\) random variates by comparing the median difference in execution time.

    Solution 
    x <- rnorm(1000)
microbenchmark::microbenchmark(
  diff1(x),
  diff2(x)
  )
    ## Unit: microseconds

  12. The following function assesses whether all elements is a logical vector are TRUE.

    all2 <- function(x) {
# function to calculate whether all elements are TRUE
# returns a scalar
# x is a logical vector
sum(x) == length(x)
}

    1. Calculate the following and benchmark all2() against R’s built-in function all(), which does the same.

      n <- 1e4
x1 <- !logical(n)
      Solution 
      all2(x1)
      ## [1] TRUE
      all(x1)
      ## [1] TRUE
      microbenchmark::microbenchmark(
  all2(x1),
  all(x1)
)
      ## Unit: microseconds

      We see that both take a similar amount of time.

    2. Now swap the first element of x1 so that it’s FALSE and repeat the benchmarking.

      Solution 
      x1[1] <- FALSE
all2(x1)
      ## [1] FALSE
      all(x1)
      ## [1] FALSE
      microbenchmark::microbenchmark(
  all2(x1),
  all(x1)
)
      ## Unit: nanoseconds

      Now all2() is much slower. This is because it’s performed a calculation on the entire x1 vector, whereas all() has stopped as soon as it’s found a FALSE.

    3. Evaluate the function any2() below against R’s built-in function any() similarly.

      any2 <- function(x) {
# function to calculate whether any elements are TRUE
# returns a scalar
# x is a logical vector
sum(x) > 0
}
      Solution 
      x2 <- logical(n)
any2(x2)
      ## [1] FALSE
      any(x2)
      ## [1] FALSE
      microbenchmark::microbenchmark(
  any2(x2),
  any(x2)
)
      ## Unit: microseconds

      We again see that both take a similar amount of time.

    4. Now swap the first element of x2 so that it’s FALSE and repeat the benchmarking.

      Solution 
      x2[1] <- TRUE
microbenchmark::microbenchmark(  
  any2(x2),
  any(x2)
)
      ## Unit: nanoseconds

      This time any2() is much slower, for similar reasoning to all2() being much slower than all(), except that any() is stopped when it reaches a TRUE.